【代数学とは?】
数や行列のように演算を持った集合を一般に「代数系」と呼びます。代数学とは代数系の学問であるとも言えます。
数に関する様々な問題を扱う「整数論」や、図形を「環」と呼ばれる代数系と結びつけて調べる「代数幾何学」等は代数学の代表的なテーマです。代数系は自然科学の諸分野においても、周期性や対称性を記述する概念として広く活躍しています。代数系のこうした側面に注目した研究は「表現論」と呼ばれます。
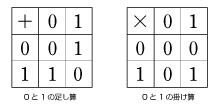
【1+1=0?】
0と1だけからなる代数系もあります。上の表が何を意味するか分かりますか?この単純で奇妙な代数系は、当時19歳の天才数学者ガロアによって代数方程式に関する深い定理と結びつけられました。19世紀に誕生したこの「ガロア理論」は、今日でも最も美しい数学理論の一つとされています。また、整数論や代数幾何学の最先端の結果を動員して近年やっと証明された「フェルマーの最終定理」は、350年もの間未解決の予想でした。
代数学には時代を越えて色褪せない数学の美しさと奥深さが詰まっています。